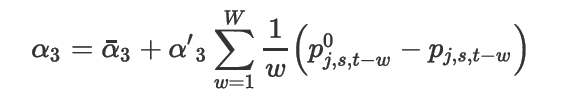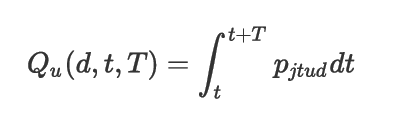电竞之家_品味电竞生活移动版

并且，据我们所知，所有现有的模型都有这样或者那样的局限性。在本节剩下的部分我们考虑两个价格差异模型，这两个模型是根据美国超市（特别是 Safeway 在芝加哥子公司的数据）的数据设计并在这些数据上做过验证的。

文献 [KJ05] 提出了这一模型，该模型的目标是联合优化基于包装大小的数量折扣和店铺级别的区域价格。这一模型与我们在需求预测章节中讨论的模型非常相似，只是该模型引入了更多的包装大小和折扣参数。

让我们考虑这样一种情况：一个零售商运营多个店铺，销售的某种产品也有几种品牌，产品的规格也有几种，例如可口可乐和百事可乐分别有 2 听装、4 听装和 6 听装。目标是优化每种包装的单位产品价格，这里假设单位产品价格是可以根据产品规格和店铺来调整。我们从标准的多元逻辑特模型（multinomial logit – MNL）开始，这一模型在前一节需求预测中讨论过。

它表示顾客在时间 t 在商店 s 购买产品 j 的概率，J 是产品的数量（所有品牌的所有规格加上）。时间以相对较长的时间间隔（如周）进行测量。参数变量 x 可以使用以下回归模型进行估计：

此处 zj 是产品规格，Pjts 是价格，djts 是折扣力度（单位美元），ruts 整合了诸如最近竞争商店等竞争性因素，而 fjts 则整合了环境变化因素如天气。因此， 回归参数 αk 基本上对应着客户对品牌、规格的偏好、对价格的敏感性、对折扣的响应度、对竞争者的偏好、对变化因素的敏感性，以及折扣对价格敏感性的影响等等。

文献 [KJ05] 认为促销案例中的价格敏感性回归模型应该比以上仅用一个回归量来表达价格敏感性更复杂，因为客户会有囤积产品的情况，这就使得过去的促销会提高其对当前产品价格的敏感性。这一方面可以通过将相应的回归器分解为两个部分来建模，如下所示：

以上公式中 α3 是平均敏感度而第二项则表示记忆效应。其中 W 是表示历史深度，即过去的周数，p0 表示常规价格，而 p 是实际的折后价格。类似的，也有观点认为对促销的敏感性也与最近的促销有关：

此处 wj 是最近的促销活动过去的周数。促销敏感性对 wj 依赖基于以下假设，两次促销之间的周期越长，则对促销的响应度越高。

公式（4.3）允许我们预测销售量，所以价格优化问题能够根据公式（4.1）分时间周期来定义：

以上公式中 cjt 表示批发价格，而 Qjt 表示预测的销售量。此处的优化约束条件是为了避免由市场竞争或者客户行为等主要因素的变化引起的剧烈的价格变化和偏移。

文献 [KJ05] 提出了这一特殊的约束条件，这一约束要求优化后的产品份额加权平均价格（表示产品的市场份额）不会超过优化前的份额加权平局价格（表示原始价格）。这一优化问题（4.4）可以在店铺水平上得到求解，这意味着在规格和地点上都可以做差异化，或者仅在连锁店级别上来差异化数量折扣。

尽管上面的模型在店铺层面做价格差异也隐含了客户层次上的价格差异，但是这一模型不是为单个客户的折扣优化来设计的。

接下来我们考虑文献 [JT13] 提出的另一种模型，这一模型是为了专门优化个性化折扣和优惠券的。这一模型的主要优势是它不仅是优化折扣的粒度，同时也尝试为指定用户提供折扣的最优时间和折扣的最优有效期。

这些时间属性上的优化思想来自于以下假设：一个客户购买的概率不是随时间恒定的，而是会随着时间变化的，因此对每一个用户而言都存在最优的折扣时间窗口。

这一模型的主要缺陷是其只能对特定品牌如厂商促销来进行优化，而不能用于品类管理。你为了对折扣的时间属性建模，假设对产品的折扣力度为 d，我们将客户 u 在时间 t 购买产品的概率分解为购买产品的概率和客户在在时刻 t 购买的概率乘积：

对给定产品的购买概率密度函数能够用公式（4.3）中用过的 MNL 的模型来估计。在时刻时购买的概率密度函数在文献 [JT13] 中由厄兰分布来建模：

此处参数变量 yu 可以用回归模型来估计，该回归模型与公式（4.3）中用来估计参数变量的类似，会用一个回归量来描述折扣力度，因此之后可以对其进行优化。

上面定义的购买概率使得我们能够对给定客户的销售量 Qu 作为折扣力度（以美元为单位）、折扣起始时间、和折扣周期的函数来建模：

以上推导可以使得我们导出如下毛利率优化问题：

这里 m 是在正常价格下的毛利率。以上公式中的第一项对应着收入，收入由三个方面组成（促销前的收入、促销期间的收入和促销后的收入）；第二项对应着营销活动的成本。下图描述了这一优化问题：

顶部的第一个图显示了客户 u 购买的概率密度函数曲线，此图中对于给定产品在正常价格时的销量对应着 S0 区域。一个固定的永久折扣增加的销量对应的区域为 S1，因此总收入和促销成本（如中间的图所示）是与 S0 和 S1 成正比的。